Home » Interview coding problems/challenges

Length of the Longest Bitonic Subsequence

Length of the Longest Bitonic Subsequence: Here, we are going to learn how to find out the length of the longest Bitonic subsequence using Dynamic programming? Submitted by Souvik Saha, on February 10, 2020

Description

This is a standard interview problem to find out the length of the longest Bitonic subsequence using Dynamic programming.

Problem statement

Given an array, you have to find out the length of the longest bitonic subsequence from the array. A bitonic sequence is a sequence where numbers of that sequence are sorted and they are increasing first then decreasing.

Note: A sorted increasing sequence is also a bitonic sequence and similarly sorted decreasing sequence is a bitonic sequence.

    Input:
    Test Case T
    T no. of lines with the value of N and corresponding values.
    E.g.
    3
    5
    1 4 2 5 7

    8
    1 7 3 2 5 4 8 1

    17
    1 10 9 3 5 4 11 7 4 8 9 6 19 5 7 8 2

    Constrains:
    1≤ T ≤ 10
    1≤ N ≤ 100
    1≤ A[i] ≤ 1000
    Output:
    Print the length of the bitonic subsequence.

Example

    T = 3
    N = 5
    1 4 2 5 7
    4 (1 2 5 7)

    N = 8
    1 7 3 2 5 4 8 1
    5 (1 3 5 4 1)

    N = 17
    1 10 9 3 5 4 11 7 4 8 9 6 19 5 7 8 2
    9 (1 3 4 7 8 9 6 5 2)

Explanation with example

Let, N be the number of elements say, X₁, X₂, X₃, ..., X_n

Now, possible counting can be:

1. The number of elements is present only in the increasing sequence.
2. The number of elements is present in both increasing and decreasing sequences.
3. The number of elements presents only in the decreasing sequence.

To find out the length of the bitonic subsequence we follow up these steps,

1. Calculate the longest increasing subsequence from the begging of the array. To find out the longest increasing subsequence we take a new array and initialize it with 1. We start our algorithm with the second column.
   Every time we check if any element is lesser then the current element. If this happens then we add up one with the value of that index in the new array and compare with the value of the current element's index in the new array and take the maximum value.
   
   
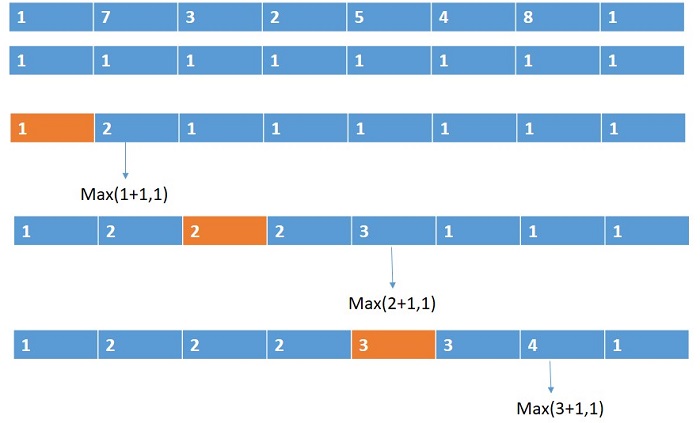
2. Calculate the longest increasing subsequence from the rear of the array.
3. Add up the value of the two arrays and minus by one because in the first longest increasing sequence it is counted and next time from the rear it also counted.
4. Take the maximum value from there.

For this sequence:

Longest increasing subsequence from front:

Longest increasing subsequence from rear:

After add up:

Therefore, the answer is 5.

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int t;

    cout << "Test Case : ";
    cin >> t;

    while (t--) {
        int n;

        cout << "Number of elements : ";
        cin >> n;

        int a[n];

        cout << "Enter the elements : ";
        //taking the elements into the array
        for (int i = 0; i < n; i++) {
            cin >> a[i];
        }

        int f[n], l[n];
        //initiate the new arrays
        for (int i = 0; i < n; i++) {
            f[i] = 1;
            l[i] = 1;
        }

        //calculate the LIS from front
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (a[j] < a[i])
                    f[i] = max(f[i], f[j] + 1);
            }
        }

        //calculate the LIS from behind
        for (int i = n - 2; i >= 0; i--) {
            for (int j = n - 1; j > i; j--) {
                if (a[j] < a[i])
                    l[i] = max(l[i], l[j] + 1);
            }
        }

        int m = 0;
        //adding the two arrays to join them
        for (int i = 0; i < n; i++) {
            m = max(m, f[i] + l[i] - 1);
        }

        cout << "Length of the sequence : " << m << endl;
    }
    return 0;
}

Output

Test Case : 3
Number of elements : 5
Enter the elements : 1 4 2 5 7
Length of the sequence : 4
Number of elements : 8
Enter the elements : 1 7 3 2 5 4 8 1
Length of the sequence : 5
Number of elements : 17
Enter the elements : 1 10 9 3 5 4 11 7 4 8 9 6 19 5 7 8 2
Length of the sequence : 9