Home » Interview coding problems/challenges

Dice throw

Dice throw: Here, we are going to learn about the solution of dice throw problem – which is an interview coding questions featured in any rounds of top companies. Submitted by Radib Kar, on February 19, 2020

Description

In this article, we are going to see a dynamic programing problem which can be featured in any interview rounds.

Problem statement

Given n dice each with m faces, numbered from 1 to m, find the number of ways to get sum X. X is the summation of values on each face when all the dice are thrown.

    Input:
    n=3
    m=3
    X=6

    Output:
    Total number of ways are: 7

Explanation

    Total number of dices: 3 say x1,x2,x3
    Number of faces on each dice: 3 (1 to 3)
    Total sum to be achieved: 6
    We will write as xi(j)which means face value of dice xi is j 
    So sum 6 can be achieved in following ways:
    6=x1(1)+x2(2)+x3(3)
    6=x1(1)+x2(3)+x3(2)
    6=x1(2)+x2(2)+x3(2)
    6=x1(2)+x2(3)+x3(1)
    6=x1(2)+x2(1)+x3(3)
    6=x1(3)+x2(2)+x3(3)
    6=x1(3)+x2(3)+x3(1)

    This are total 7 ways to achieve the sum.

Solution Approach

If it was only 1 dice, then if X<=m, the answer would be 1 else 0. Since there is only one way to achieve the sum if possible as there is only one dice.

Now when n, number of dice>1, then the problem becomes a recursive one

We can think of the recursive function as f(n,X) where n is number of dice and X is desired sum.

A single dice has m choices, which means the face can have values ranging 1 to m
So,

Recursively we can write,

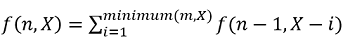
That means summation of all choices for this particular dice to have face value 1 to minimum(X, m)

For our example case, n=3, m=3, X=6

So, we need to find f(3,6)

    f(3,6)=f(2,5)+f(2,4)+f(2,3)

f(2,5), f(2,4), f(2,3) all are sub problems themselves which are needed to be solved further. This would generate a recursion tree.

Of course, we have base cases for single dice which is f(1,i)=1 for i=1 to m

But this recursion will generate many overlapping sub problems, hence, we need to convert it to dynamic programing.

    1)  Declare dp[n+1][x+1] similar to f(n,x). Initialize it to 0.
    2)  Implement the base case f(1,i)
        for i=1 to i minimum(m ,x)
            dp[1][i]=1;
    3)  Fill the other values as per recursion relation
        for i=2 to n //iterate for number of dices
            for j=1 to x //iterate for sums
                for k=1 to minimum(m ,j)
                    //iterate for face values up to minimum(m,j),j be the subsum
                    dp[i][j]+=dp[i-1][j-k];
                end for
            end for
        end for    

    4)  The answer is dp[n][x]

C++ Implementation

#include <bits/stdc++.h>

using namespace std;

long long int dicethrow(int m, int n, int x) {
  if (m * n < x)
    return 0;

  long long dp[n + 1][x + 1];
  memset(dp, 0, sizeof(dp));

  //base case
  for (int i = 1; i <= m && i <= x; i++)
    dp[1][i] = 1;

  for (int i = 2; i <= n; i++) { //iterate for number of dices
    for (int j = 1; j <= x; j++) { //iterate for sums
      //iterate for face values up to minimum(m,j),j be the subsum
      for (int k = 1; k <= m & k < j; k++) {
        dp[i][j] += dp[i - 1][j - k];
      }
    }
  }
  return dp[n][x];

}
int main() {
  int n, m, x;

  cout << "Enter number of dices, n:\n";
  cin >> n;
  cout << "Enter number of faces on a dice, m:\n";
  cin >> m;
  cout << "Enter sum, X:\n";
  cin >> x;
  cout << "Number of ways to achieve sum: " << dicethrow(m, n, x) << endl;

  return 0;
}

Output

RUN 1:
Enter number of dices, n:
3
Enter number of faces on a dice, m:
3
Enter sum, X:
6
Number of ways to achieve sum: 7

RUN 2:
Enter number of dices, n:
3
Enter number of faces on a dice, m:
3
Enter sum, X:
12
Number of ways to achieve sum: 0

In the second output there is no way to acquire the sum which can be verified as m*n<X. It's better practise to keep such base case to optimize your code :)