Home » Interview coding problems/challenges

Longest Repeating Subsequence

Longest Repeating Subsequence: Here, we are going to learn about the solution of Longest Repeating Subsequence – which is an interview coding questions featured in any rounds of top companies.
Submitted by Radib Kar, on February 21, 2020

Description:

This question has been featured in interview rounds of Amazon.

Problem statement:

Given string str, find the length of the longest repeating subsequence such that the two subsequences don't have the same character in the same position, i.e., any i^th character in the two sub-sequences shouldn't have the same index in its original string.

    Let the string be,
    Str="includehelpisbest"
    
    Output will be:
    Longest repeating sub-sequence length is 3
    The longest repeating sub-sequence is:"ies"

The output is given above where the repeating sub-sequences are in two different colours. One more repeating subs-sequence can be,

Solution Approach:

The problem can be solved in similar way as longest Common subsequence problem, where input to LCS() would be String str both the case. That is

    LRS(str) = LCS(str,str) which some constraints

Let's discuss the recursive approach first.

Let,

    
    l = Length of the  string,str
    f(l,l) = Longest repeating subsequence length for string length l

Now,

Think of the following example,

Say the string is: x₁x₂...x_l

Say,

x_i==x_j and i≠j (this is the constraint what we discussed above)

Then obviously we need to find LCS for the remaining part of string (x₁x₂...x_i-1, x₁x₂...x_j-1) and then add 1 for this valid character match (repeating character match),

Else

Maximum of two case,

1. LCS of the string leaving character x_i,x₁x₂...x_i-1 and string x₁x₂...x_j.
2. LCS of the string x_l1, x₁x₂...x_i and second string leaving character x_j,x₁x₂...x_j-1

Now, we need to recur down to 0. So,

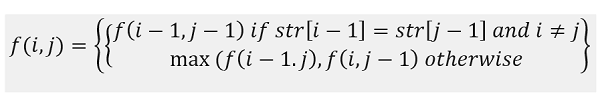
Where base cases are,

    f(0,i)=0 for 0≤i≤l
    f(i,0)=0 for 0≤i≤ l

If you generate this recursion tree, it will generate many overlapping sub-problems and thus, we need to reduce the re-computing. That's why we need to convert it into dynamic programming where we will store the output of the sub-problems and we will use it to compute bigger sub-problems.

Converting to Dynamic programming:

    1)  Initialize dp[l+1][l+1]  to 0
    2)  Convert the base case of recursion:
        for i=0 to l
            dp[i][0]=0;
        for i=0 to l
            dp[0][i]=0;

    3)  Fill the DP table as per recursion.
        for i=1 to l    //i be the subproblem length for first string of LCS
            for j=1 to l //j be the subproblem length for second string of LCS
                if(i≠j and str1[i-1]==str2[j-1]) //xi==xj  and i≠j
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
            end for
        end for  
    4)  The final output will be dp[l][l]

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

void print(vector<int> a, int n)
{
    for (int i = 0; i < n; i++)
        cout << a[i] << " ";
    cout << endl;
}

int max(int a, int b)
{
    return (a > b) ? a : b;
}

int LRS(string str1, string str2)
{
    int l = str1.length();
    int dp[l + 1][l + 1];

    //base case
    for (int i = 0; i <= l; i++)
        dp[i][0] = 0;
	
    for (int i = 0; i <= l; i++)
        dp[0][i] = 0;
	
    //fill up
    for (int i = 1; i <= l; i++) {
        for (int j = 1; j <= l; j++) {
            if (i != j && str1[i - 1] == str2[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
    }

    return dp[l][l];
}

int main()
{
    string str;

    cout << "Enter the string:\n";
    cin >> str;
    cout << "Longest repeating sub-sequence length: " << LRS(str, str) << endl;

    return 0;
}

Output

Enter the string:
includehelpisbest
Longest repeating sub-sequence length: 3