Home » Interview coding problems/challenges

Number of ways to construct the grid

Here, we are going to learn the solution to find the number of ways to construct the grid – which is a recursion problem featured in Amazon interview rounds. Submitted by Radib Kar, on April 19, 2020

Problem statement

There is a grid with size NX4 and you have only one type of tiles to construct the grid. You can place either vertically or horizontally. You need to find, how many ways you can construct a grid of size N x 4 using the 1X4 tiles.

    Input:
    Input contains only one line with the value of N.

    Output:
    Print number of possible ways.

    Constraints:
    1 ≤ N ≤ 80

Example

    Input:
    1

    Output:
    1

    Explanation:
    So n=1 and grid is 1X4. That’s why only one way we can build

    Input:
    4

    Output:
    2

    Explanation:
    So, n=4 and grid is 4X4. That's why two way we can build

    First way is to place all four tiles horizontally one after one
    Like below,
    

    

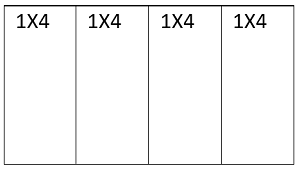
    Second way is to place all four tiles vertically one after one

    Input:
    5
    
    Output:
    3

    Explanation:
    So, n=5 and grid is 5X4. That's why two way we can build
    First way is to place all five tiles horizontally one after one
    Second way is, place four tiles vertically and place the last 
    tiles horizontally above them
    Third way is, place the first tile horizontally and place other 
    four tiles vertically on that.

Solution Approach

The problem is recursive by nature and thus can be solved recursively.

Let,

    f(n)=Total number of ways of constructing the grid

So, obviously f(n) would be

f(n)=f(n-1) +f(n-4) as we can either place last tile horizontally on the previous tiles or we can construct by vertically placing 4 1X4 blocks.

So let's say f(8)

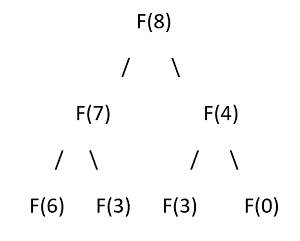
So on...

So, there are so many overlapping sub-problems and that's why we need to store and use Dynamic programming.

So, if we convert it into a DP solution,

    1)  Declare dp[n+1] to store results for input n.
    2)  Initialize dp[0]=1,dp[1]=1,dp[2]=1,dp[3]=1;
    3)  for i=4 to n
            dp[i]=dp[i-1]+dp[i-4];
    4)  Return dp[n];    

So dp[n] is the final result.

C++ Implementation

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int n, item;

    cout << "Enter value of n" << endl;
    cin >> n;

    long long int* dp = (long long int*)(malloc(sizeof(long long int) * (n + 1)));

    dp[0] = 1;
    dp[1] = 1;
    dp[2] = 1;
    dp[3] = 1;

    for (int i = 4; i <= n; i++)
        dp[i] = dp[i - 1] + dp[i - 4];

    cout << "Number of ways to make the tile is: " << dp[n] << endl;

    return 0;
}

Output

Enter value of n
5
Number of ways to make the tile is: 3