Home » Digital Electronics

Half & Full Subtractors, Design Full Subtractor Using Half Subtractors

In this tutorial, we will learn about the half and full subtractors, designing of full subtractor using half subtractor in Digital Electronics. By Saurabh Gupta Last updated : May 11, 2023

A Subtractor is a digital circuit which performs subtraction operation.

What is a Half Subtractor?

It is a combinational circuit that performs subtraction of two binary bits. It has two inputs (minuend and subtrahend) and two outputs Difference (D) and Borrows (B_out). We use half-subtractor to subtract the LSB of the subtrahend to the LSB of the minuend when one binary number is subtracted from another. Subtraction is done according to the rule of binary subtraction and the operations can be summarized in a truth table as,

A	B	Difference (D)	Borrow (Bout)
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

K-Map Simplification

We use K-Map to obtain the expression for Difference and Borrow bit which is as,

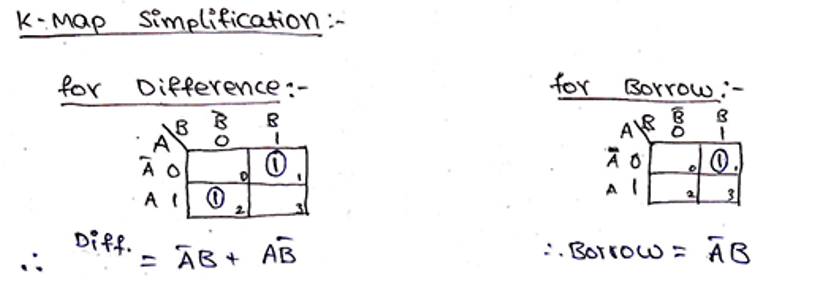
On solving the K-Map and getting the simplified Boolean Expressions we can observe that Boolean expression for Difference (D) is the same as the XOR operation and which is the same as what we get as the expression of Sum in Half Adder and Boolean expression for Borrow (B_out) is A.B

Hence, Logic circuit diagram for Half-Adder can be drawn as,

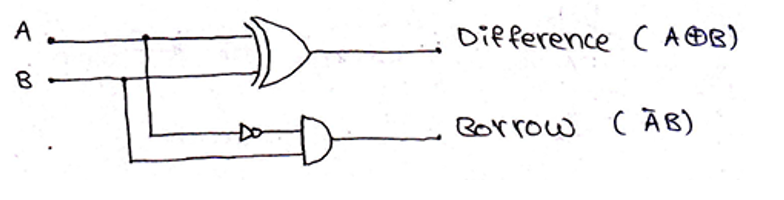
What is a Full Subtractor?

Full Subtractor also belongs to the class of a combinational circuit and is used to perform subtraction of two binary bits. The half-subtractor can only be used for subtraction of LSB bits, but if there occurs a case of borrow during subtraction of LSB bits, then it can have affected over subtraction in higher columns. Thus, we have a total of three inputs (two original bits and third is considering the borrow (B_in) of the previous stage) and two outputs Difference (D) and Borrow (B_out) respectively. The Truth Table of Full Subtractor can be written as,

A	B	Bin	Difference (D)	Borrow (Bout)
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

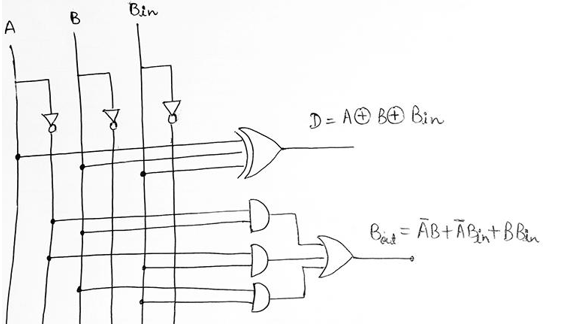
K-Map Simplification

We use K-Map to obtain the expression for Difference and Borrow bit which is as,

After solving K-Map, simplified Boolean Expressions for Difference is A ⊕ B ⊕ B_in and for Borrow it is A.B + A.B_in + B. B_in, thus, logic circuit diagram for full-subtractor can be drawn as

Designing of Full Subtractor using Half-Subtractors

A Full-Subtractor can also be implemented using two half-subtractors and one OR gate. The circuit diagram for this can be drawn as,

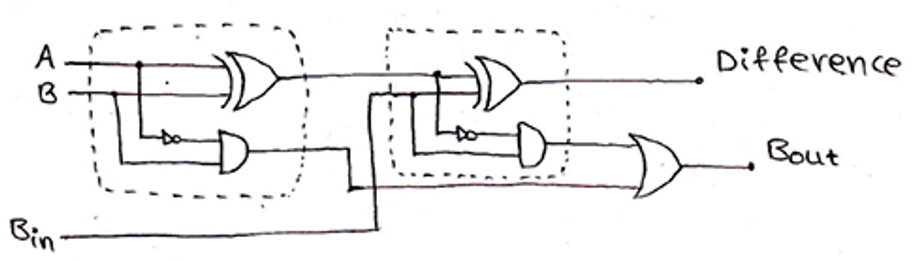
The Boolean expressions for Difference and Borrow are,

Difference  = A ⊕ B ⊕ Bin
Borrow      = ( (A ⊕ B) ). Bin + A. B
    = (A. B + A.B). Bin + A. B
    = A. B. Bin + A.B. Bin + A. B
    = A. B. Bin + B (A. Bin + A )		[Since, A + BC = (A+B) (A+C)]
    = A. B. Bin + B. [(A + A) (Bin + A)]	[Since, A + A = 1]
    = A. B. Bin +B. Bin + B. A
    = Bin ( A. B + B) + B. A		[Since, A + BC = (A+B) (A+C)]
    = Bin [(A + B) (B +  B)] + B. A		[Since, B + B = 1]
    = A. Bin + B. Bin + B. A

---