Home » Discrete Mathematics

Discrete Mathematics Functions, Their Types, and Examples

In this tutorial, we will learn about the functions in discrete mathematics, their types, and examples. By Prerana Jain Last updated : May 09, 2023

Functions in Discrete Mathematics

Suppose, X and Y are two any sets. A relation f from X to Y is said to be a function. If for every x E X there is a unique y E Y such that (x, y) E f. A function is a special case of the relation. The term such as "transformation", "mapping", "correspondence" and "operations" are used as synonyms for "function". The notation f: X → Y.

X → Y is used to express f as a function from X to Y. For a function f: X → Y if (x,y) E f then x is called an argument and the corresponding y is called the image of x under f. Instead of writing (x, y) e f, it is customary to write y= f(x) and to call y the values of the function f at x.

Example (f) : A -> B

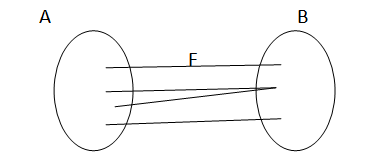
• A is called domain of f.
• B is called codomain of f.
• The range is the set containing all images of the elements of an under function f. It is denoted by f(a).
• Range of f = { f(n) | x E A}
• Range of f C= B codomain

Types of Functions

1. Constant Function

The function f defined in a set X such that f(x) = a, xEX, is called a constant function. In other word f: X → Y is a constant function if the range of f consists of only one element. This can be represented by a diagram.

2. One-to-One (Injective)

A mapping f of X into Y is said to be injective or one-to-one mapping. If distinct elements of X have distinct images in Y. It is called injective.

The f: X → Y is a (one-to-one) mapping, if and only if:f(x1) = f(x2) => x1 = x2

In other words f: X → Y is one-to-one (or injective) mapping, whenever x1 = x2 then,

F(x1) not equals to f(x2), where, x1, x2 belongs to X.

Thus a mapping from a set X into a set Y is one-to-one or injective, if each element of Y has at least one element of X mapping into Y.

3. Into Mapping

A mapping f: A → B is said to be into mapping, if f(A) is a proper subset of B. In this case, we say that f maps A into B.

4. Onto Function (Surjective)

If the mapping f: X → Y is such that every element of Y is the image of at least one element of X then the mapping is called an onto or surjective mapping. In other words, the mapping f: X → Y is onto, if given yEY there exists an element xEX such that y = f(x).

5. One-to-One (Bijective) Function

A mapping which is one-to-one as well as onto is called Bijective or one-to-one onto mapping.

To determine whether a mapping is Bijective, we follow the following procedure.

• To show that f is one-to-one we must show that
  f(x1) = f(x2) => x1 = x2
• To show that f is onto we must show that for each yEY, there exists an xEX such that f(x) = y.
  Then, it is one-to-one onto mapping. The sets X and Y have the same number of elements.

6. Invertible Function

A function f: X → Y is said to be invertible. If there exists a function g: y → X such that: Fog = ty and gof = tx

Where Ix and Iy are the identify maps. In such a case the function g is called the inverse of f and is denoted by f^-1.

---