Home » Digital Electronics

Examples of Designing of Arbitrary Sequence Counters and Bidirectional Counter

In this tutorial, we will learn how we can design counters which can count in some random sequence and the steps to design these types of counters with an example. Also, we will also read about the designing process of bidirectional counters. By Saurabh Gupta Last updated : May 11, 2023

Arbitrary Sequence Counters Design Examples

Example 1

Design a modulo-5 counter to count the random sequence 0,1,3,7,6. Design should include circulatory to ensure that if we end in any unwanted state. The next clock pulse will reset the counter to zero. Implement the circuit using T-flip-flops.

Solution

Follow the following steps to design a modulo-5 counter:

Step 1: The number of flip-flops required to design a mod-5 counter can be determined by using the equation: 2ⁿ >= N, where n is equal to the number of flip-flops and N is the mod number. In this case, the possible value on n which satisfies the above equation is 3. Hence, the required number of flip-flops is 3.

Step 2: Drawing the state diagram. Here, in the given sequence used states are: 0,1,3,7,6 and the unused states are: 2,4,5. For those unused states, the next state must be zero. Hence, a state diagram can be drawn as:

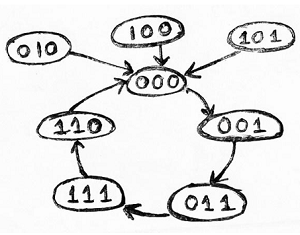
Step 3: Using the excitation table of T flip-flop, we need to obtain the flip-flop inputs for each state that we obtained in step 2 and now we will enter it into a table as:

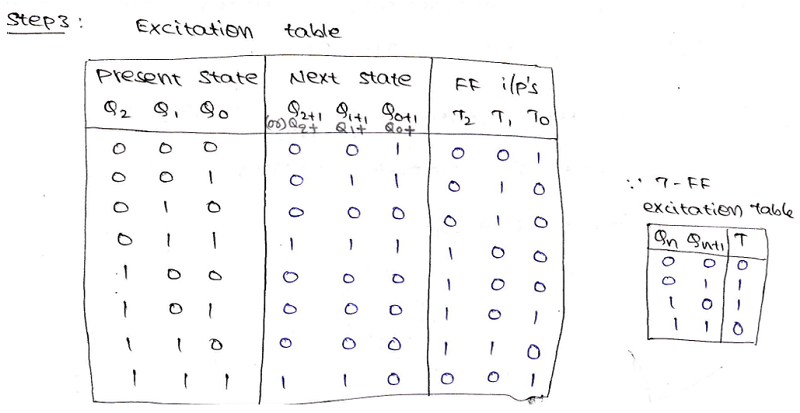
Step 4: Making K-Map for each input combination and simplifying it to get the minimized Boolean expression.

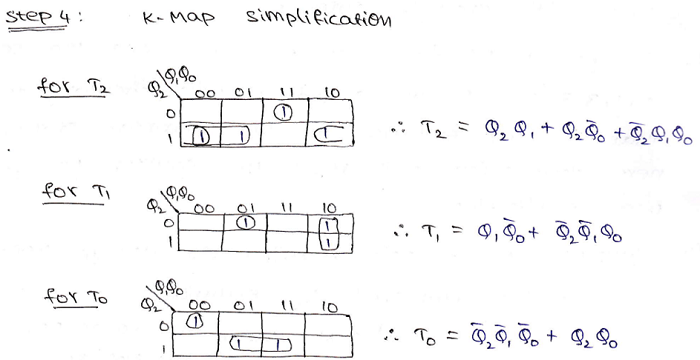
Step 5: Using the Boolean expressions obtained in step 4, now we will draw the required counter circuit which can be shown as:

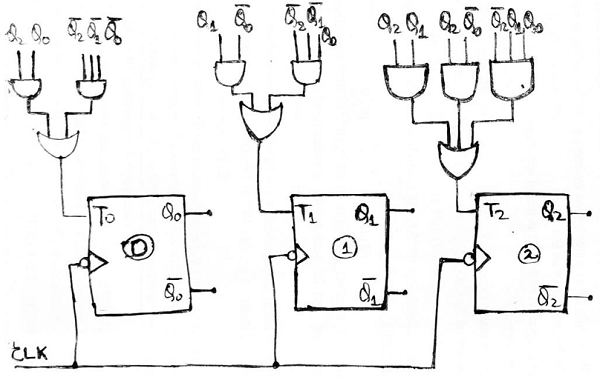
Note: Q₂ is the MSB bit and Q₀ is the LSB bit.

Example 2

Design a synchronous counter to count the following sequence 7,4,3,1,5,0,7,4,3,... Implement the circuit using T-flip-flops.

Solution

Step 1: Total number of states is 6. Therefore, the number of flip-flops required to design the counter can be determined by using the equation: 2ⁿ >= N, where n is equal to no. of flip-flop and N is the mod number. In this case, the possible value on n which satisfies the above equation is 3. Hence, the required number of flip-flops is 3.

Step 2: Drawing the state diagram. Here, in the given sequence used states are: 7,4,3,1,5,0 and the unused states are: 2 and 6. For those unused states, the next states are treated as don’t cares. Hence, a state diagram can be drawn as:

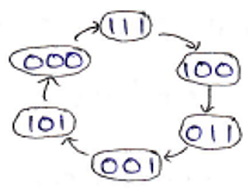
Step 3: Using the excitation table of T flip-flop, we need to obtain the flip-flop inputs for each state that we obtained in step 2 and now we will enter it into a table as:

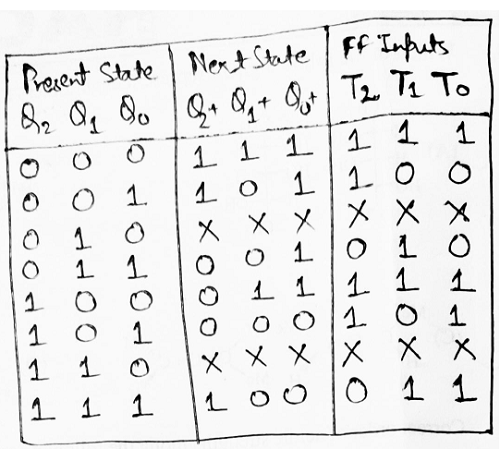
Step 4: Making K-Map for each input combination and simplifying it to get the minimized Boolean expression.

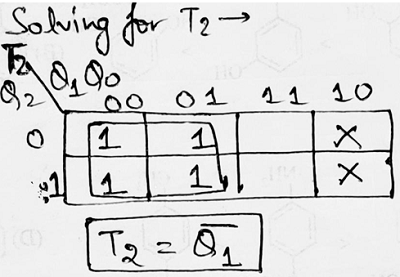
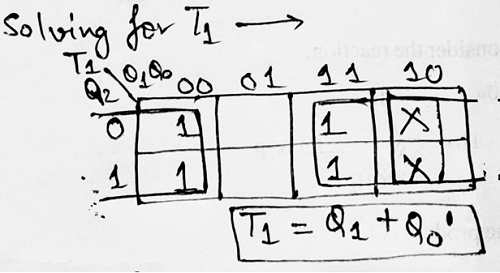
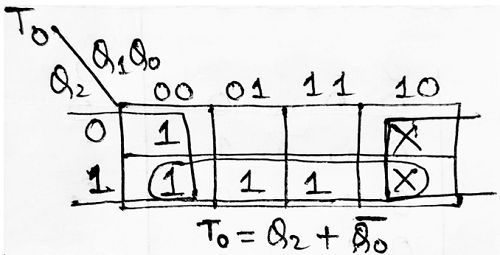
Step 5: Using the Boolean expressions obtained in step 4, now we will draw the required counter circuit which can be shown as:

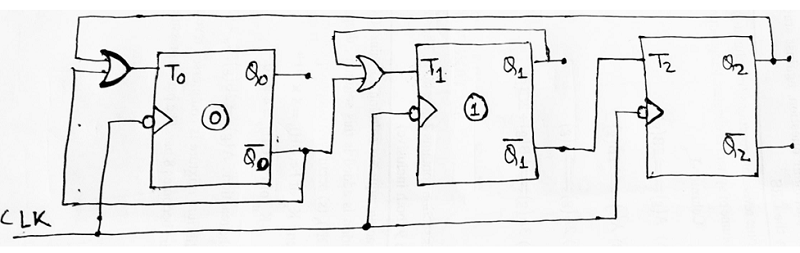
Designing of Up/Down counter (or) Multimode counter (or) Bidirectional Counter

The counter which is capable of progressing in either direction i.e., in ascending order (incrementing order) or descending order (decreasing order) through a certain counting sequence is known as an up/down Counter.

Usually, Up/Down operation of the counter is controlled by a mod (M) signal. When M=1, the counter follows the up sequence (0,1,2, 3, ..., n).

And when M=0, the counter goes through the down sequence (n, n-1, n-2, ..., 1, 0)

Example 3

Design a 3-bit synchronous up/down counter or bidirectional counter using T flip-flop.

Solution

Step 1: The number of flip-flops required is: 3 (since a 3-bit counter needs to be designed.)

Step 2: The type of flip-flop being used is T flip-flop.

Step 3: Drawing the state diagram:

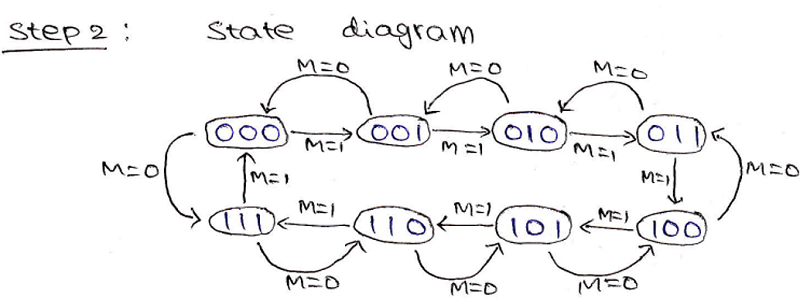
Step 4: Draw the excitation table:

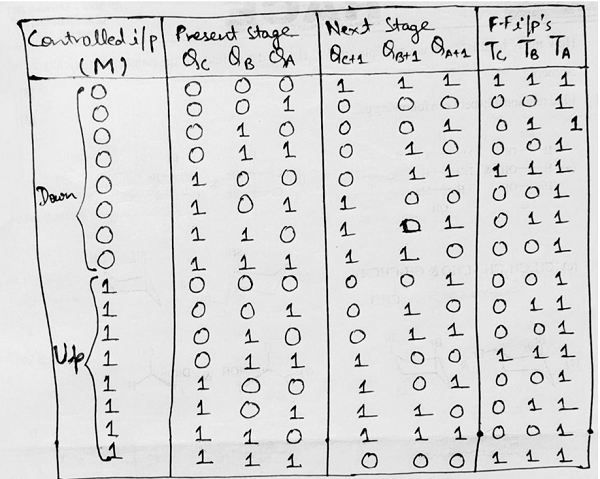
Step 5: Making K-Map for each input combination and simplifying it to get the minimized Boolean expression.

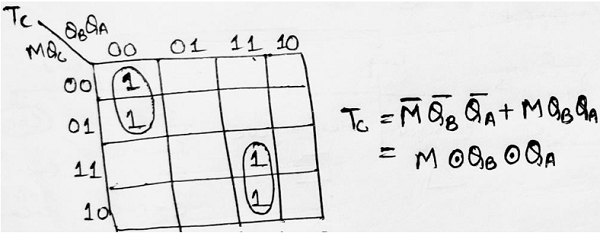
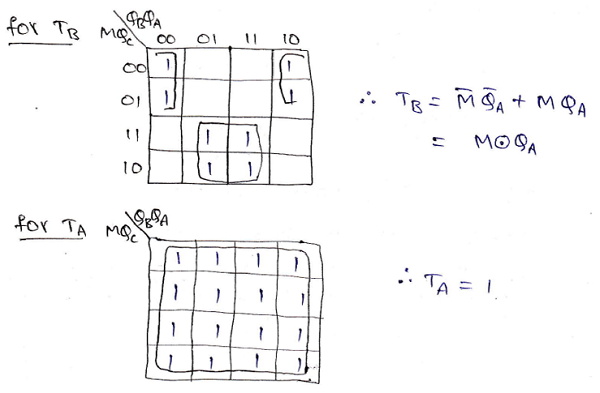
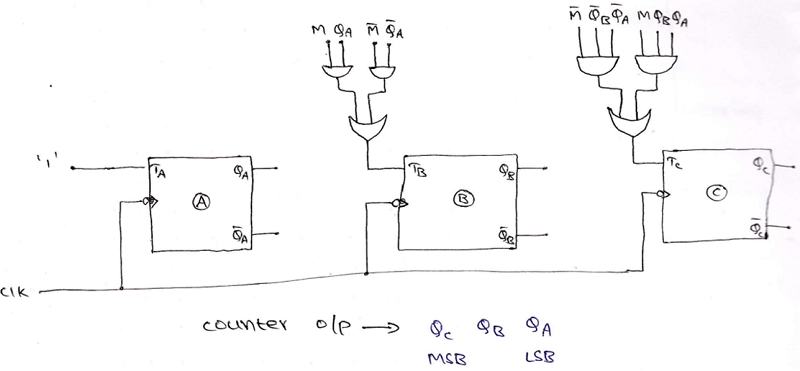
Step 6: Using the Boolean expressions obtained in step 5, now we will draw the required counter circuit which can be shown as:

---