Home »
Digital Electronics
Excess-3 (XS-3) Code and Gray Code
Excess-3 (XS-3) Code and Gray Code: In this tutorial, we are going to learn about the Excess-3 and gray codes with examples.
By Saurabh Gupta Last updated : May 10, 2023
Excess-3 Code
Excess-3 Code is a non-weighted BCD (8421) Code. Excess-3 Code is derived from 8421 code by adding 0011 (3) to all code groups. It is a sequential code, thus can be also used for performing arithmetic operations. Also, Excess-3 codes are self-complementing codes in nature. Therefore, subtraction by the method of complement addition is more direct in the XS-3 code than in 8421 BCD code. Like, BCD code, it also has six invalid states which are: 0000, 0001, 0010, 1101, 1110 and 1111.
Relationship Between Decimal, Binary, and XS-3 Numbers
The relationship between decimal numbers, binary numbers, and XS-3 numbers can be given as,
| Decimal Numbers | Binary Numbers | Excess-3 Code (Binary Number + 0011) |
|---|
| 0 | 0000 | 0011 |
| 1 | 0001 | 0100 |
| 2 | 0010 | 0101 |
| 3 | 0011 | 1100 |
| 4 | 0100 | 0111 |
| 5 | 0101 | 1000 |
| 6 | 1010 | 1001 |
| 7 | 0111 | 1010 |
| 8 | 1000 | 1011 |
| 9 | 1001 | 1100 |
Example: Represent (1548)10 in Excess-3 notation.
Solution
1 = 0001 + 0011 = 0100 5 = 0101 + 0011 = 1000
4 = 0100 + 0011 = 0111 8 = 1000 + 0011 = 1011
Therefore, (1548)10 = 0100 1000 0111 1011 in XS-3 form.
Gray Code
The Gray Code is a non-weighted code and is cyclic as well. It is referred to as cyclic because successive code words in this code differ by only one bit-position i.e., it is a unit distance code. It is also reflective. In many practical applications such as analog to digital conversion, unit distance codes are used.
Conversion of Binary Code into Gray Code
To convert Binary Code into Gray Code, one should have knowledge of truth table of XOR Gate which is as,
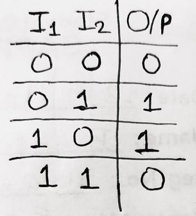
Now, the MSB of the binary number is copied as it is and then we perform XOR operation for consecutive bits in a pair of two.
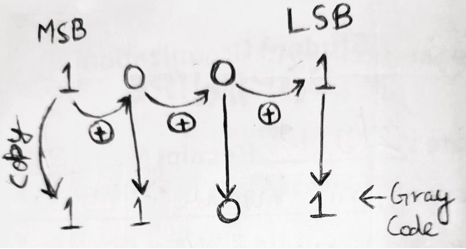
Example 1: Convert (1001)2 into Gray Code
Solution
Therefore, (1001)2 = (1101)g in gray code.
Example 2: Convert (10)10 into Gray Code
Solution
Firstly, we convert decimal number to binary number and then convert binary to gray code.
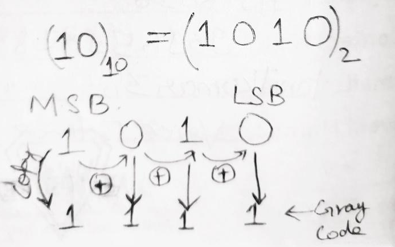
Therefore (10)10 = (1111)g
Conversion of Gray Code into Binary Number
The MSB of Gray code is copied as it to be the MSB bit of binary number which is then XORed with the next bot of gray code, the result is recorded as the next bit of binary number, now this recorded bit is XORed with the next bit of gray code and this process is continued till the LSB is obtained.
Example 1: Convert (110011100)g to binary number
Solution
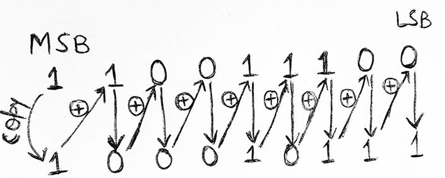
Therefore, (110011100)g = (10010111)2
Example 2: Convert (101010101)g to binary number
Solution
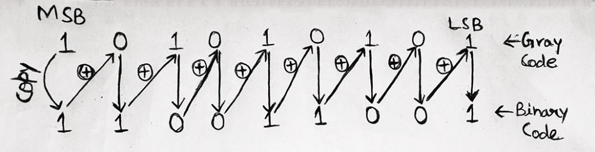
Therefore, (101010101)g = (110011001)2
Advertisement
Advertisement