Home » Digital Electronics

Karnaugh Maps with Don't Care Conditions

In this tutorial, we will learn about the Karnaugh maps with don't care conditions in Digital Electronics. By Saurabh Gupta Last updated : May 10, 2023

What are Don't Care Conditions?

Till now, the Boolean expressions which have been discussed by us were completely specified, i.e., for each combination of input variable we have specified a minterm by representing them as 1 in the K-Map. But, there may arise a case when for a given combination of input we may not have a specified output or the input combination may be invalid. The combinations for which we don't have any output expression specified are called don't care combination.

Example

For Example, in 8421 code, input states 1001, 1010, 1011, 1100, 1101, 1110 and 1111 are invalid and the corresponding output is the don't care. Similarly, in Excess-3 code, binary input states 0000, 0001, 0010, 1101, 1110 and 1111 are unspecified and are also represented by don't care.

Don't care combinations in the K-Map

These don't care combinations in the K-Map are denoted by an X (cross) symbol.

The X is called "Don't care conditions".

Rules for Karnaugh Maps with Don't Care Conditions

General rules to be followed while minimizing the expressions using K-Map which include don't care conditions are as follows,

1. After forming the K-Map, fill 1's at the specified positions corresponding to the given minterms. Fill X at the positions where don't care combinations are present.
2. Now, Encircle the groups in the K-Map. One thing to be kept in mind is, now we can treat Don't Care conditions (X) as 1s if these help in forming the largest groups. No such group can be encircled whose all the elements are X.
3. If still there are 1s left which doesn't get encircled in any of the groups, then these isolated 1s are encircled individually.
4. Now, recheck all the encircled groups, and remove any redundancy if present.
5. Write the Boolean expression for each encircled group.
6. The final minimal expression can be obtained by ORing each Boolean expressions that were obtained from each group.

Point to remember

While designing K-Map using SOP form, don't care conditions (X) are considered as 1, if it helps form the largest group, otherwise it is considered as 0 and are left during encircling. On the contrary, while designing a K-Map using POS form, don't care conditions (X) are considered as a 0, if it helps form the largest group, otherwise it is considered as 1 and are left during encircling.

Karnaugh Maps with Don't Care Conditions Examples

Example 1

Minimize the given Boolean Expression by using the four-variable K-Map.
F (A, B, C, D) = Σ m (1, 5, 6, 12, 13, 14) + d (2, 4).

Solution

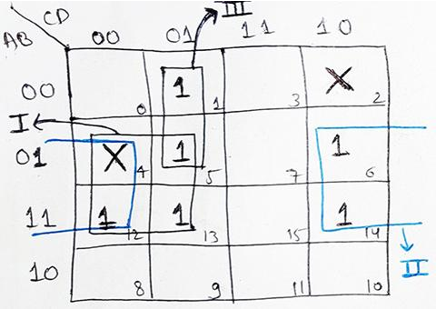
We will fill 1s at the appropriate minterm positions and also the don't care positions will be filled with (X). Now, we can encircle these 1s and X using the rules we have discussed earlier. We can observe that we can encircle them into three groups. First Group (encircled by black ink) contains four 1s and the Boolean expression given by it is B.C. Second group is the rolling group (encircled by blue ink) which also contains four 1s gives B.D. Third group is the pair of 1s which gives A.C.D

Hence, the resultant simplified Boolean Expression will be:

F (A, B, C, D) = B.C + B.D + A.C.D

Example 2

Minimize the given Boolean Expression by using the four-variable K-Map.
F (A, B, C, D) = Σ m (1, 5, 6, 12, 13, 14) + d (2, 4).

Solution

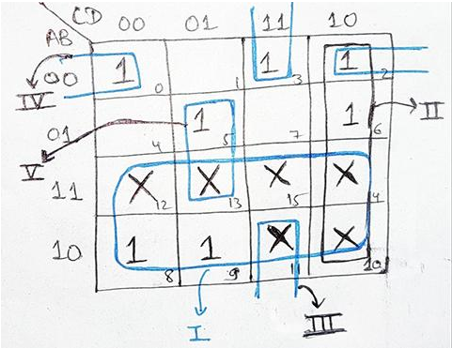
As we have already discussed in our last example, we will fill 1's at the appropriate minterm positions and X at don't care positions, encircling the groups using the rules we have discussed above results into the formation of five groups as seen in the image. The Boolean Expressions given by the groups are A, C.D, B.C. D, A.B.D and B.C.D respectively.

ORing these individual Boolean expressions to get the simplified Boolean Expression as:

F (A, B, C, D) = A + C. D + B.C. D + A.B. D + B. C. D

---