Home » Digital Electronics

Half & Full Adders, Design Full Adder Using Half Adder

In this tutorial, we will learn about the half and full adders, designing of a full adder using half adder in Digital Electronics. By Saurabh Gupta Last updated : May 11, 2023

Half Adder

The logic circuit which performs the addition of 2 bits is called Half- Adder. It is a kind of combinational circuit. It contains two binary inputs "augend" and "addend" and two binary outputs Sum and Carry.

The Sum bit (S) and the Carry bit (C) are given according to the rules of Binary Addition which can be summarized in the form of truth table as,

A	B	Sum (S)	Carry (C)
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

K-Map Simplification

We use K-Map to obtain the expression for Sum and Carry bit which is as,

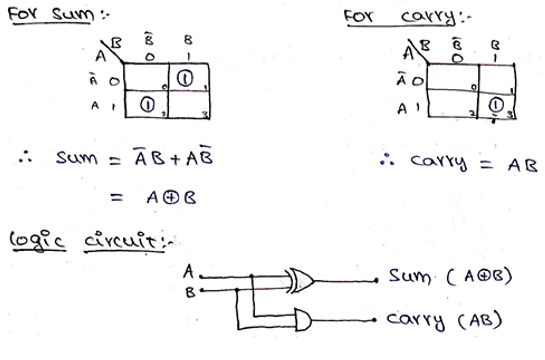
Upon obtaining the Boolean expressions, we can observe that Boolean Expression for Sum is nothing but the Exclusive OR function for two inputs and the Boolean Expression for carrying is the same as AND function. Thus, the circuit diagram for Half Adder can be drawn using an XOR gate and AND gate as shown in the above image.

Full Adder

Full Adder is an arithmetic circuit which performs the arithmetic sum of 3-input bits. It consists of 3 inputs and 2 outputs. One additional input is the Carry bit (C) in which represents the carry from the previous significant position.

Similarly, as in Half-Adder, we have two outputs Sum (S) and Carry (C), which can be obtained using the rules of Binary Addition and can be summarized in a Truth Table as,

A	B	C	Sum (S)	Carry (C)
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

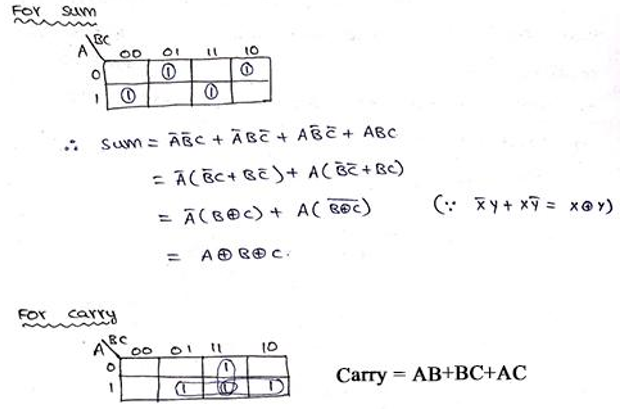
K-Map Simplification

We use K-Map to obtain the expression for Sum and Carry bit which is as,

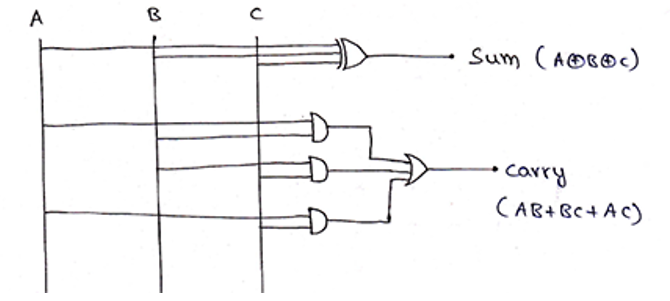
The logic circuit for Full Adder can be drawn as,

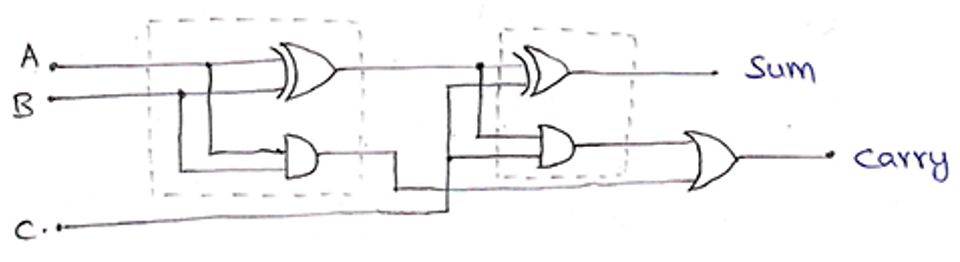
Full Adder using Half Adder

A Full Adder can also be implemented using two half adders and one OR gate.

The circuit diagram for this can be drawn as,

And, it could be represented in block diagram as,

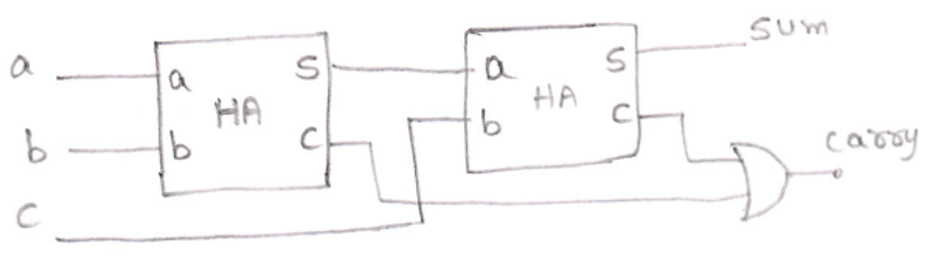
The Boolean expression for Sum and Carry is as,

Sum     = A ⊕ B ⊕ C
Carry   = AB + (A ⊕ B). C
        = AB + ( A. B + A. B). C
        = AB + A. BC + A. B. C
        = B (A + A. C) + A. B. C
        = B [(A+ A) (A + C)] + A. B. C
        = AB + AC + A. B. C
        = AB + C (B + A. B)
        = AB + C [(B + A) (B + B)]
        = AB + BC + AC

---