Home » Digital Electronics

Solved Examples on Reduction of Boolean Expression

Examples on Reduction of Boolean Expression: Here, we have set of some of the Solved Examples on Reduction of Boolean Expression. By Saurabh Gupta Last updated : May 10, 2023

Example 1: Simplify the given Boolean Expression to minimum no. of variables or literals

1. (A+B). (A+B)
2. ABC + AB + ABC

Answer

1) (A+B). (A+B)

= A.A + A. B + B.A + B.B
= A + A. B + B.A + 0
= A (1 + B + B) = A

2) ABC + AB + ABC

= ABC + ABC + AB
= AB (C + C) +  AB
= AB +  AB
= B (A + A) = B. 1 = B

Example 2: Prove that: (A + C) (A.B +C) = 0

Solution

LHS = A.(A + C) (A.B + C)
    = (A. A + AC) (A.B + C)
    = AC (A.B + C)		[Since, A.A = 0]
    = AC. A.B + AC. C
    = 0 = RHS			[Since, A. A = 0 and C. C = 0]
Hence, our result is proved.

Example 3: Reduce the expression (B +BC) (B + BC) (B + D)

Solution

= (B +BC) (B + BC) (B + D)
= (BB +BBC) (B + D)
= (B +0) (B +D)		[Since, B.B =0]
= BB +BD			[Since, B.B =1]
= B + BD
= B (1+D) =B 		[Since, 1+D =1].

Example 4: Reduce the expression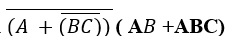

Solution

= A.BC. (AB +ABC)		        [De-Morgan's Law]
= A.BC (AB+ABC)
= A.BC. AB + A.BC. ABC
= A.A.B.B.C + A.A.B.B.C.C		[Manipulation]
= 0 + 0 = 0

Example 4: Prove the Associative Law for XOR operation

Solution

We know that XOR operation is given as: A⊕B = AB + AB

To prove associativity for XOR operation we are required to prove:

(A⊕B) ⊕C =A⊕(B⊕C). Therefore,

From equation 1 and 2 we can see LHS = RHS, thus associative law holds true for XOR operation.

---