Home » Digital Electronics

Karnaugh Maps (K-Maps): Meaning, Types, Representations

Karnaugh Maps (K-Maps): In this tutorial, we will learn about the Karnaugh Maps, the different types of Karnaugh Maps: 2 variables K-Map, 3 variables K-Map, and 4 variables K-Maps, their representations using SOP and POS forms. By Saurabh Gupta Last updated : May 10, 2023

In the previous articles, we have already discussed how we can use theorems of Boolean Algebra to simplify Boolean functions so that these simplified expressions help us in getting simple, less expensive and smaller circuits. Although, that method was helpful but also was difficult and non-systematic. We don't have any guarantee that we have reached a minimal expression. Thus, Karnaugh Maps (K-Maps) are used to simplify Boolean functions. K-Map is a systematic method to simplify Boolean expressions.

Karnaugh Map (K-Map)

A K-Map is a chart or graph composed of an arrangement of adjacent cells. Each of the cells represents one of the 2² possible products that can be formed from n-variables.

Types of Karnaugh Maps (K-Maps)

Two different types of K-Map can be drawn for both CSOP and CPOS in terms of respective minterms and maxterms.

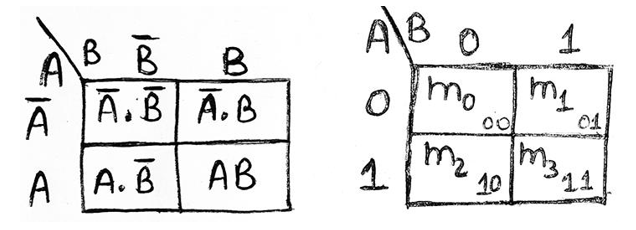
1) 2-variable K-Map

A 2-variable expression can have 2² = 4 possible ways of input representation. Thus, a 2-variable K-Map will have 4 adjacent cells representing each of the 4 possible combinations of inputs. Binary numbers at the top of the K-Map represent the condition of variable B along any column and binary number to the left of the K-Map represents the condition of variable A along any row.

Representation using minterms (SOP form)

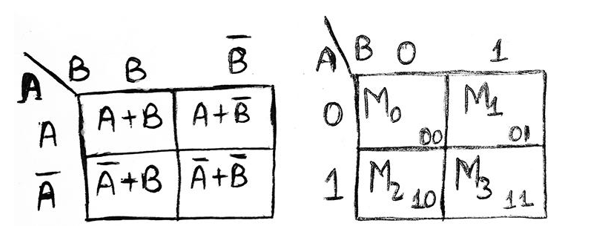
Representation using maxterms (POS form)

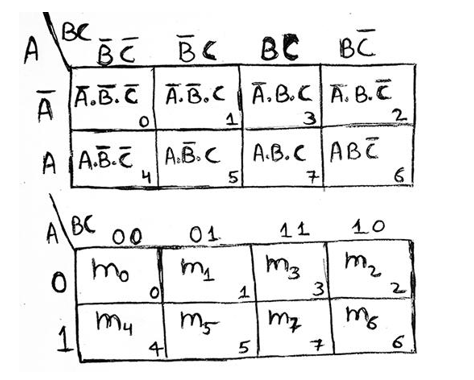
2) 3-variable K-Map

A 3-variable expression can have 2³ = 8 possible ways of input representation. Thus, a 3-variable K-Map will have 8 adjacent cells representing each of the 8 possible combinations of inputs.

The thing to be noticed in the representation is that the binary numbers along the top of the K-Map are not in normal binary order. They are, in fact, in the Gray Code. This is to ensure that two physically adjacent squares are adjacent i.e., their minterms and maxterms differ by only one variable.

Representation using minterms (SOP form)

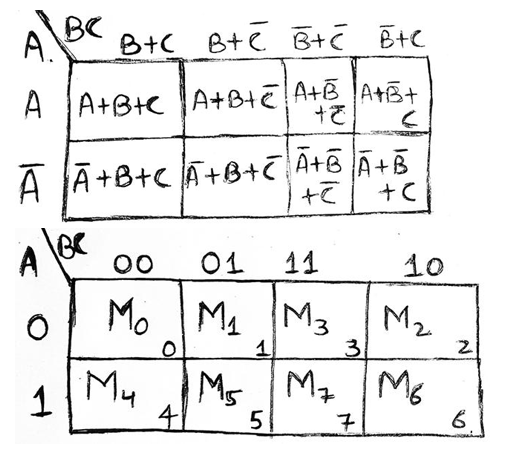
Representation using maxterms (POS form)

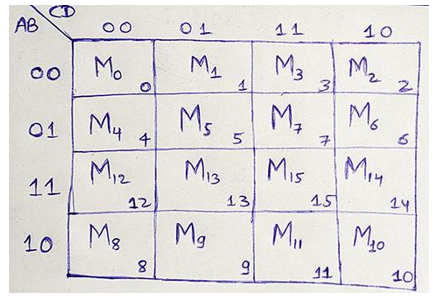
3) 4-variable K-Map

A 4-variable expression can have 2⁴ = 16 possible ways of input representation. Thus, a 4-variable K-Map will have 16 adjacent cells representing each of the 16 possible combinations of inputs.

The binary number designations of the rows and columns are in Gray Code. Binary numbers at the top of the K-Map represents the condition of variables C and D along any column and binary numbers to the left of the K-Map represents the condition of variables A and B along any row.

Representation using minterms (SOP form)

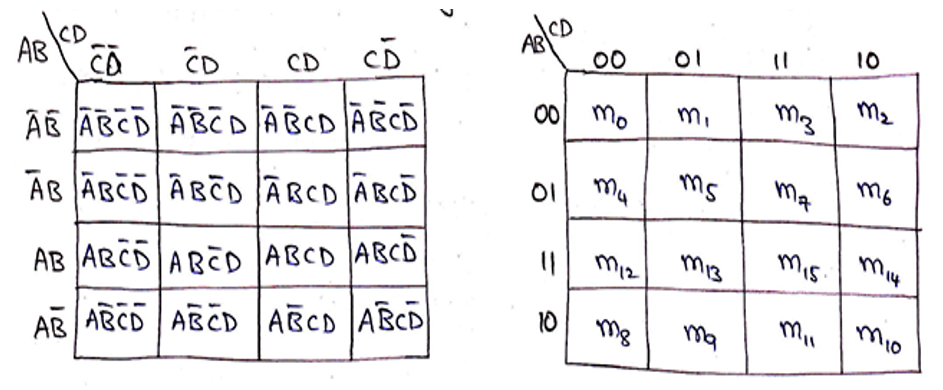
Representation using maxterms (POS form)

---