Home »
Digital Electronics
Combinational Circuits and Its Design Procedure
In this tutorial, we will learn about combinational circuits in digital electronics, their design procedure, and the difference between combinational circuits and sequential circuits.
By Saurabh Gupta Last updated : May 11, 2023
What are Combinational Circuits?
The combinational circuits are the network of logic gates having input independent variables and output variables which depend only on the present value of the input variables and are not dependent upon their previous values. These combinational circuits do not have any memory elements associated with them. There is another class of digital circuits known as the sequential circuit which have memory elements associated with them and thus the output of these sequential circuits depends both on present inputs and past outputs which are stored in the memory elements. Input and output relationship of combinational circuits can be represented as,

Design Procedure of a Combinational Circuits
- Step 1: From the specifications of the circuit, determine the required number of inputs and outputs and assign a symbol to each.
- Step 2: Derive the truth table that defines the relation between input and output.
- Step 3: Obtain the simplified Boolean function for each output as a function of the input variables using the Karnaugh Map.
- Step 4: Draw the logic diagram and verify the correctness of the design.
Combinational Circuits Example
The insurance policy will be issued only to person, if he/she is,
- A married female of 22 years or more or,
- A female under 22 years, or
- A married male under 22 years and who has not been involved in any road accident, or
- A married male who has been involved in a car accident, or
- A married male of 22 years old or above who has not been involved in any car accident.
Design the combinational logic circuit using K-Map and obtain the simplest Boolean Expression for the given problem which can help the applicant to issue the insure policy.
Solution
From the above question, we can infer that, we must have four input variables and one output variable. Let the input variables be A, B, C, and D and the output variable be Y.
The input variables are,
- The person is married or not. Let the logic be represented by symbol A and gives 1 if the person is married and 0 if the person is not married.
- The person is male or female. Let the logic be displayed by symbol B and gives 1 if the person is male and 0 if the person is female.
- The person's age is above 22 years or not. Let the logic be displayed by symbol C and gives 1 if the person is below 22 years age and 0 if the person is 22 years or above.
- The person is involved in a road accident. Let the logic be displayed by symbol D and gives 1 if the person has been involved in a road accident and 0 if the person has not been involved in a road accident.
The output variable Y gives 1 if the person is issued insurance policy otherwise Y will be 0 if the applicant does not get the insurance policy.
Truth Table
Hence, we can derive a truth table, from all the above situations which can be displayed as,
| A | B | C | D | Y |
|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Hence, we can draw a K-Map to get the simplified Boolean expression to represent the required logic as,
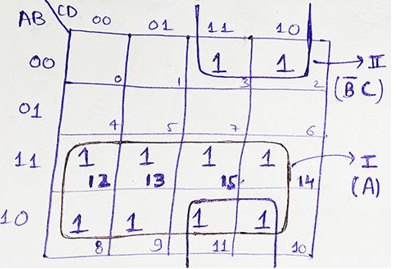
F (A, B, C, D) = A + B. C
Difference Between Combinational Circuits and Sequential Circuits
The main differences between combinational circuits and sequential circuits can be summarized are:
| S.N. |
Combinational Circuits |
Sequential Circuits |
| 1 |
Outputs only depends on present inputs. |
Outputs depends on present inputs as well as past outputs. |
| 2 |
It does not contain any internal memory. |
It contains internal memory. |
| 3 |
It only contains logic gates. |
It contains both logic gates and memory elements. |
Advertisement
Advertisement