Algorithms MCQs (Multiple-Choice Questions) and Answers

1. The primary approach used by the Merge Sort algorithm is ____.

1. Dynamic programming
2. Greedy approach
3. Divide-and-conquer
4. Backtracking

Answer: C) Divide-and-conquer

Explanation:

Merge Sort follows the divide-and-conquer approach.

Divide-and-conquer - This approach divides the array into smaller subarrays, sorts each subarray, and then merges them back together.

Discuss this question

2. What is the best-case time complexity of the Merge Sort algorithm?

1. O(n)
2. O(n log n)
3. O(n^2)
4. O(log n)

Answer: B) O(n log n)

Explanation:

Merge Sort has a best-case time complexity of O(n log n), the same as its average and worst-case complexities.

Discuss this question

3. Which of the following is a disadvantage of the Merge Sort algorithm?

1. It is not stable.
2. It has a worst-case time complexity of O(n^2).
3. It is not an in-place sorting algorithm.
4. It cannot handle large datasets.

Answer: C) It is not an in-place sorting algorithm.

Explanation:

Merge Sort requires additional memory to store the merged subarrays. So, it is not an in-place sorting algorithm.

Discuss this question

4. What is the space complexity of Merge Sort?

1. O(1)
2. O(log n)
3. O(n)
4. O(n^2)

Answer: C) O(n)

Explanation:

Merge Sort requires additional space proportional to the size of the array being sorted, leading to a space complexity of O(n).

Discuss this question

5. Which of the following is a real-world application of Merge Sort?

1. Prim's algorithm
2. Sorting large datasets
3. Depth-first search
4. None of the above

Answer: B) Sorting large datasets

Explanation:

Merge Sort is particularly useful for sorting large datasets.

Discuss this question

6. What type of graph edges does Dijkstra's Algorithm not handle correctly?

1. Parallel edges
2. Negative weights
3. Zero-weight edges
4. All of the above

Answer: C) Zero-weight edges

Explanation:

Dijkstra's Algorithm fails with graphs with negative weight edges because it assumes that once a node's shortest path is found, it cannot be improved, which is not true in the presence of negative weights.

Discuss this question

7. The data structure primarily used to implement Dijkstra's Algorithm is ____.

1. Stack
2. ArrayList
3. Priority Queue
4. Linked List

Answer: C) Priority Queue

Explanation:

A Priority Queue efficiently extracts the minimum distance vertex and updates the shortest paths in Dijkstra's Algorithm.

Discuss this question

8. The best-case time complexity of Dijkstra's Algorithm is ______.

1. O(V^2)
2. O(E + V)
3. O(V + E log V)
4. O(E log V)

Answer: D) O(E log V)

Explanation:

When using an adjacency list along with a priority queue, the time complexity of Dijkstra's Algorithm is O (E log V), where:

1. E is the number of edges
2. V is the number of vertices.

Discuss this question

9. One of the best applications of Dijkstra's Algorithm is_____.

1. Google Maps
2. Predicting weather patterns
3. Sorting a list of numbers
4. None of the above

Answer: A) Google Maps

Explanation:

Dijkstra's algorithm finds shortest paths in Google Maps.

Discuss this question

10. Which of the following problems cannot be solved using Dijkstra's Algorithm?

1. Shortest path in a city map
2. Optimal network routing
3. Handling graphs with negative weight cycles
4. Efficient airline route planning

Answer: C) Handling graphs with negative weight cycles

Explanation:

Dijkstra's Algorithm does not work correctly with graphs with negative weight cycles.

Discuss this question

11. What is the primary goal of Kruskal's Algorithm?

1. To find the shortest path between two vertices
2. To find the minimum spanning tree for a connected weighted graph
3. To sort all edges of a graph in descending order
4. To traverse a graph using a depth-first search

Answer: B) To find the minimum spanning tree for a connected weighted graph

Explanation:

Kruskal's Algorithm is designed to find a subset of the edges that form a tree including every vertex, where the total weight of all the edges in the tree is minimised.

Discuss this question

12. In Kruskal's algorithm, first sort all graph edges in increasing order.

1. True
2. False
3. Can't say anything
4. Your choice

Answer: A) True

Explanation:

In Kruskal's algo, the first step is sorting all the edges of the graph in increasing order.

Discuss this question

13. The time complexity of Kruskal’s algorithm is ____.

1. O (E log E)
2. O (V log V)
3. O (VE)
4. None of the above

Answer: A) O (E log E)

Explanation:

The time complexity of Kruskal’s algorithm is O (E log E) , where E stands for edges.

Discuss this question

14. Kruskal algorithm is considered a _____.

1. Greedy algorithm
2. Brute force approach
3. Two-pointer approach
4. None of the above

Answer: A) Greedy algorithm

Explanation:

Kruskal's Algorithm is considered a greedy algorithm because it makes decisions at each step based on the immediate best choice without considering the global optimal solution.

Discuss this question

15. What happens if adding an edge creates a cycle in the spanning tree?

1. The edge is added to the spanning tree
2. The algorithm restarts
3. The edge is discarded
4. The edge's weight is increased

Answer: C) The edge is discarded

Explanation:

If an edge creates a cycle in the spanning tree, it is discarded to ensure the tree remains acyclic.

Discuss this question

16. Which data structure is primarily used in Breadth-First Search (BFS) to keep track of the vertices to be visited?

1. Stack
2. Queue
3. Priority Queue
4. Linked List

Answer: B) Queue

Explanation:

BFS uses a queue data structure to maintain the order in which nodes are to be visited.

Discuss this question

17. What is the time complexity of Breadth-First Search (BFS) in a graph with 𝑉V vertices and EE edges?

1. O(V^2)
2. O(E + V)
3. O(V + E)
4. O(E * V)

Answer: C) O(V + E)

Explanation:

The time complexity of BFS is O(V + E) because it visits each vertex and each edge once.

Discuss this question

18. In BFS, what condition indicates the presence of a cycle in an undirected graph?

1. If a node is visited twice during traversal.
2. If the graph is connected.
3. If the graph has more edges than vertices.
4. If a node has no adjacent nodes.

Answer: A) If a node is visited twice during traversal.

Explanation:

In an undirected graph, if BFS encounters a node that has already been visited (and it is not the immediate parent node), it indicates the presence of a cycle.

Discuss this question

19. Fill in the blank: BFS is particularly useful for finding the ____ in an unweighted graph.

1. Shortest path
2. Longest path
3. Minimal spanning tree
4. Maximum flow

Answer: A) Shortest path

Explanation:

BFS is used to find the shortest path in an unweighted graph because it explores all nodes at the present "depth" level before moving on to nodes at the next depth level.

Discuss this question

20. Which of the following is NOT an application of Breadth-First Search (BFS)?

1. Shortest path finding in an unweighted graph
2. Topological sorting in a directed acyclic graph
3. Level order traversal of a binary tree
4. Finding the minimum spanning tree

Answer: D) Finding the minimum spanning tree

Explanation:

BFS is not used to find the minimum spanning tree. Algorithms like Kruskal's and Prim's are used for finding the minimum spanning tree.

Discuss this question

21. What is the time complexity of the Karatsuba algorithm for multiplying two binary strings?

1. O(n^2)
2. O(n^1.59)
3. O(n log n)
4. O(n)

Answer: B) O(n^1.59)

Explanation:

The Karatsuba algorithm uses divide-and-conquer to reduce the number of required multiplications, leading to an O time complexity (n^1.59).

Discuss this question

22. True or False: The Karatsuba algorithm can be applied to any numerical base, not just binary.

1. True
2. False
3. Can't say
4. None

Answer: A) True

Explanation:

The Karatsuba algorithm is a general multiplication technique that can be applied to numbers in any base, though it's often demonstrated with binary numbers.

Discuss this question

23. The classical method of binary multiplication has a time complexity of ____.

1. O(n log n)
2. O(n^2)
3. O(n)
4. O(n^1.59)

Answer: B) O(n^2)

Explanation:

The classical method of binary multiplication involves iterating through each bit of the second number and performing shifts and additions, so a time complexity of O(n^2).

Discuss this question

24. Which of the following is NOT a step in the Karatsuba algorithm?

1. Divide the input strings into halves
2. Recursively compute the product of the halves
3. Multiply the smaller strings directly without recursion
4. Combine the results using shifts and additions

Answer: C) Multiply the smaller strings directly without recursion

Explanation:

The Karatsuba algorithm involves recursive multiplication of the halves. Direct multiplication without recursion is not a part of the Karatsuba method but could be part of the base case handling.

Discuss this question

25. The space complexity of the Karatsuba algorithm is _____.

1. O(n)
2. O(1)
3. O(n^2)
4. None of the above

Answer: A) O(n)

Explanation:

The space complexity of the Karastuba algorithm is O(n).

Discuss this question

26. What is the primary purpose of the Floyd-Warshall algorithm?

1. To find the shortest path from a single source to all other nodes
2. To find the shortest path from a single source to a single destination
3. To find the shortest paths between all pairs of nodes
4. To find the longest paths between all pairs of nodes

Answer: C) To find the shortest paths between all pairs of nodes

Explanation:

The Floyd-Warshall algorithm finds the shortest paths between all pairs of nodes in a weighted graph.

Discuss this question

27. The Floyd-Warshall algorithm can handle graphs with which type of edge weights?

1. Only positive edge weights
2. Only negative edge weights
3. Both positive and negative edge weights
4. Only zero edge weights

Answer: C) Both positive and negative edge weights

Explanation:

The Floyd-Warshall algorithm can handle graphs with positive and negative edge weights but does not work correctly with graphs containing negative cycles.

Discuss this question

28. True or False: The Floyd-Warshall algorithm works for both directed and undirected graphs.

1. True
2. False
3. Can't say
4. None

Answer: A) True

Explanation:

The Floyd-Warshall algorithm can be applied to both directed and undirected weighted graphs.

Discuss this question

29. The time complexity of the Floyd-Warshall algorithm is ______.

1. O(V^2)
2. O(V^2 + E)
3. O(V^3)
4. O(E^3)

Answer: C) O(V^3)

Explanation:

The Floyd-Warshall algorithm has a time complexity of O(V^3) due to its three nested loops over the graph vertices.

Discuss this question

30. Which of the following statements is true about the Floyd-Warshall algorithm?

1. It uses a greedy approach.
2. It uses dynamic programming.
3. It only works with unweighted graphs.
4. It can only find the shortest path for a single source.

Answer: B) It uses dynamic programming.

Explanation:

The Floyd-Warshall algorithm follows a dynamic programming approach to find the shortest paths between all pairs of nodes.

Discuss this question

31. Why is the Floyd-Warshall algorithm better suited for dense graphs rather than sparse graphs?

1. It has a lower time complexity for dense graphs.
2. It runs in constant time for dense graphs.
3. It ignores the number of edges in the graph.
4. It performs the same regardless of graph density.

Answer: C) It ignores the number of edges in the graph.

Explanation:

The Floyd-Warshall algorithm runs in O(V^3) time regardless of the number of edges.

Discuss this question

32. The Floyd-Warshall algorithm does not work correctly for graphs with ______.

1. Positive cycles
2. Zero-weight edges
3. Negative cycles
4. Directed edges

Answer: C) Negative cycles

Explanation:

The Floyd-Warshall algorithm does not work correctly for graphs containing negative cycles, as the presence of such cycles can lead to incorrect shortest-path calculations.

Discuss this question

33. Which of the following is the time complexity of the naive recursive implementation of the LCS problem?

1. O(m * n)
2. O(m^2)
3. O(2^(m+n))
4. O(m + n)

Answer: C) O(2^(m+n))

Explanation:

The naive recursive implementation has an exponential time complexity because it explores all possible subsequences.

Discuss this question

34. The Dynamic Programming approach to LCS has an auxiliary space complexity of O(1).

1. True
2. False
3. Can't say
4. None

Answer: B) False

Explanation:

The auxiliary space complexity of the standard dynamic programming approach to LCS is O(m * n), where m and n are the lengths of the input strings.

Discuss this question

35. The optimal substructure property of the LCS problem indicates that the problem can be broken down into ____.

1. Smaller unrelated problems
2. Subproblems that can be solved independently
3. Overlapping subproblems
4. Subproblems that build on the solutions of smaller subproblems

Answer: D) Subproblems that build on the solutions of smaller subproblems

Explanation:

Optimal substructure means the problem can be solved by using the solutions to its subproblems optimally.

Discuss this question

36. In the context of the LCS problem, which approach uses a 2D array to store the lengths of common subsequences?

1. Greedy Algorithm
2. Divide and Conquer
3. Dynamic Programming (Bottom-Up)
4. Backtracking

Answer: C) Dynamic Programming (Bottom-Up)

Explanation:

The bottom-up dynamic programming approach uses a 2D array to store the lengths of common subsequences.

Discuss this question

37. What is the auxiliary space complexity of the space-optimized bottom-up approach for LCS?

1. O(m * n)
2. O(n)
3. O(1)
4. O(m)

Answer: B) O(n)

Explanation:

The space-optimized approach uses two arrays of size n, where n is the length of one of the strings.

Discuss this question

38. In the LCS problem, if the last characters of the input strings are the same, the LCS length can be derived as 1 + LCS of ____.

1. Remaining parts of both strings
2. One string with the last character removed and the other string unchanged
3. Both strings unchanged
4. Remaining part of the first string and unchanged second string

Answer: A) Remaining parts of both strings

Explanation:

If the last characters are the same, we add 1 to the LCS length of the remaining parts of both strings.

Discuss this question

39. The LCS length of the strings 'ABC' and 'CBA' is 2?

1. True
2. False
3. Can't say
4. None

Answer: B) False

Explanation:

The LCS length of "ABC" and "CBA" is 1. There are common subsequences of length 1.

Discuss this question

40. What type of algorithm is Prim's algorithm?

1. Dynamic Programming
2. Divide and Conquer
3. Greedy
4. Backtracking

Answer: C) Greedy

Explanation:

Prim's algorithm is a greedy algorithm that builds the MST by selecting the minimum weight edges at each step.

Discuss this question

41. Prim's algorithm starts with an arbitrary vertex and grows the MST by adding the ____ edge that connects a vertex in the MST to a vertex outside the MST.

1. Longest
2. Shortest
3. Heaviest
4. Lightest

Answer: D) Lightest

Explanation:

At each step, Prim's algorithm selects the minimum weight edge that connects the MST to a vertex outside the MST.

Discuss this question

42. Prim's algorithm can produce different MSTs depending on the starting vertex?

1. True
2. False
3. Can't say
4. None

Answer: A) True

Explanation:

The choice of the starting vertex can lead to different MSTs, although all will have the same total weight.

Discuss this question

43. In Prim's algorithm, what data structure is commonly used to efficiently select the minimum weight edge?

1. Stack
2. Queue
3. Priority Queue
4. Linked List

Answer: C) Priority Queue

Explanation:

A priority queue helps in efficiently selecting the edge with the minimum weight at each step.

Discuss this question

44. The complexity of Prim's algorithm when using an adjacency list and a binary heap is ____.

1. O(V^2)
2. O(E log V)
3. O(E + V)
4. O(V log E)

Answer: B) O(E log V)

Explanation:

When using an adjacency list with a binary heap, Prim's algorithm runs in O(E log V) time.

Discuss this question

45. Prim's algorithm guarantees the same MST irrespective of the starting node?

1. True
2. False
3. Can't say
4. None

Answer: B) False

Explanation:

While the total weight of the MST will be the same, the structure of the MST can vary depending on the starting vertex.

Discuss this question

46. In Prim's algorithm, what is the initial key value assigned to the starting vertex?

1. Infinity
2. -1
3. 0
4. 1

Answer: C) 0

Explanation:

The starting vertex is given a key value of 0 to ensure it is picked first.

Discuss this question

47. In the adjacency matrix representation, the time complexity of Prim's algorithm is ____.

1. O(V log E)
2. O(V^3)
3. O(V^2)
4. O(E^2)

Answer: C) O(V^2)

Explanation:

When using an adjacency matrix, the time complexity of Prim's algorithm is O(V^2) due to the need to check all edges for the minimum weight edge selection.

Discuss this question

48. What is the primary purpose of Kadane's Algorithm?

1. To find the shortest path in a graph
2. To find the largest sum of a contiguous subarray
3. To sort an array
4. To find the minimum sum of a contiguous subarray

Answer: B) To find the largest sum of a contiguous subarray

Explanation:

Kadane's Algorithm is used to find the subarray with the largest sum within a given array.

Discuss this question

49. The time complexity of Kadane's algorithm is ____.

1. 0(n)
2. O(log n)
3. O(n^2)
4. None of the above

Answer: A) 0(n)

Explanation:

The time complexity of Kadane’s algorithm is O(n).

Discuss this question

50. For a given array, what will be the maximum contiguous array sum? int n[]={ -2, -3, 4, -1, -2, 1, 5, -3 };

1. -1
2. 10
3. 7
4. None of the above

Answer: C) 7

Explanation:

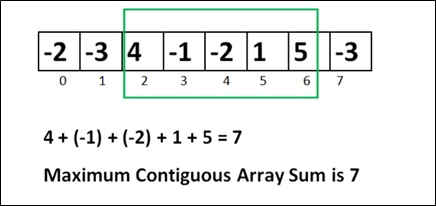
Discuss this question

51. Kadane's Algorithm can be used to find the smallest sum contiguous subarray by negating the elements of the array.

1. True
2. False
3. Can't say
4. None

Answer: A) True

Explanation:

By negating all elements in the array, Kadane's Algorithm can be used to find the smallest sum contiguous subarray.

Discuss this question

52. Which of the following statements is true about Kadane's Algorithm?

1. It finds the maximum sum of any subarray in O(N^2) time.
2. It requires additional space proportional to the size of the array.
3. It finds the maximum sum of a contiguous subarray in O(N) time.
4. It cannot handle arrays with all negative numbers.

Answer: C) It finds the maximum sum of a contiguous subarray in O(N) time.

Explanation:

Kadane's Algorithm efficiently finds the maximum sum of a contiguous subarray with a linear time complexity, O(N).

Discuss this question