Home » JavaScript

Bitwise Operators in JavaScript

JavaScript Bitwise Operators: In this tutorial, we will learn about the different types of bitwise operations in JavaScript with the help of examples. By Siddhant Verma Last updated : July 29, 2023

A lot of times you come across some strange operators where you're knocking your head to understand what is going on in the code. Almost all the programming languages have bitwise operators. It is essential for a language to have these since they work at the binary level. Let's first understand what bitwise operators are and why they are the way they are for any general language or framework then we can dive into how to use them in JavaScript. In the number system, we have more than one way of representing numbers. Most of the time we are using the decimal numbers which have a base-10 but there are other types of numbers such as hexadecimal, binary, octal, etc.

JavaScript Bitwise Operators

Bitwise operators interact with the numbers at the binary level. Since any machine understands only binary (a mere combination of the 0's and 1's), the way a machine understands what we're doing in a program is by converting into its own language of the 0's and 1's. That's why the most fundamental way of playing with numbers is by breaking them down at the binary level. When you store a variable or carry out even basic arithmetic operations, in reality, these operations are being done by first converting the base -10 numbers to binary numbers. Even variables stored in memory are referenced through binary numbers and memory addresses are themselves a hexadecimal value. So understanding Bitwise is a great way to understand how a machine is interpreting things and anything has done using them is always faster than what you'd achieve through some other operation.

Bitwise operators help us to carry out bit masking operations and play with the numbers at the binary level. We will look at the following most common bitwise operators in JavaScript.

Types of JavaScript Bitwise Operators

Operator	Description
&	JavaScript Bitwise AND
|	JavaScript Bitwise OR
^	JavaScript Bitwise XOR
~	JavaScript Bitwise NOT
<<	JavaScript Bitwise Left Shift
>>	JavaScript Bitwise Right Shift

JavaScript Bitwise Operators Explanation – Everything You Need to Know

• JavaScript stores numbers as 64 bits floating-point numbers, but all bitwise operations are performed on 32 bits binary numbers.
• Before a bitwise operation is performed, JavaScript converts numbers to 32 bits signed integers.
• After the bitwise operation is performed, the result is converted back to 64 bits of JavaScript numbers.

Let's first see what they mean by carrying out some operations. The bitwise AND first converts the two numbers into their binary and then does the AND operation (logical multiplication) from the end bit by bit.

Let's say we have two numbers; 5 and 1.
Binary of 5: 1001
Binary of 1: 0001

JavaScript Bitwise AND Operator

If we take AND of every digit from the right side we get 0001 which is 1 in decimal notation. We can simply use & to get the same result, ie, the Bitwise AND between two numbers.

To tryout, this code follow the following rules,

Open the chrome dev console to try out the examples by right clicking on the browser → selecting inspect → selecting console or simply pree f12.

You can carry out these operations to verify the results. You simply need to change the decimal numbers to their binary equivalent and perform bit by bit operation and convert the binary so obtained back to decimal.

JavaScript Bitwise OR Operator

The Bitwise OR does logical addition of two binary numbers.

JavaScript Bitwise XOR Operator

The Bitwise XOR gives 1 if the bits are different and 0 otherwise.

JavaScript Bitwise NOT Operator

The Bitwise NOT ~ simply inverses all bits of the binary representation of the number. Wherever you have a 0, you'll have a 1 and vice versa.

Notice, how NOT ~ of a number gives us the negative of that number incremented by 1? This can be logically verified concerning how the computer stores a negative number.

JavaScript Bitwise Left Shift Operator

<< or the left shift operator pushes all the bits to the right and the leftmost one falls off.

Binary of 5: 0101 5<<1=> 1010 which is the binary representation of 10.

JavaScript Bitwise Right Shift Operator

Similarly, the right shift >> operator pushes all the bits to the left and rightmost falls off.

Binary of 5: 0101 5>>1=> 0010 which is the binary representation of 2.

Let's verify these,

What if you left shift a certain number a b times? Or right shift a b times?

In general, we can say a<<b is a*(2^b). If a=5, b=2 then 5*(2^2) which gives 5*4=20.

Similarly, we can say a>>b is a/(2^b). If a=5, b=2 then 5/(2^2) which gives 5/4=1.

Okay now let's write a simple function that accepts two numbers and performs all the bitwise operations we have discussed so far.

function bitwiseOperations(a=2,b=3){
	console.log('${a} AND ${b} : ',a&b);
	console.log('${a} OR ${b} : ',a|b);
	console.log('${a} XOR ${b} : ',a^b);
	console.log('NOT ${a} : ',~a);
	console.log('NOT ${b} : ',~b);
	console.log('Left Shift ${a} : ',a<<1);
	console.log('${a} left shift ${b} : ',a>>b);
	console.log('${a} right shift ${b} : ',a<<b);
}

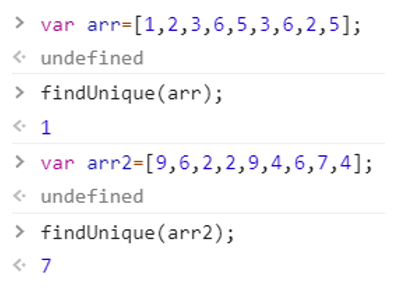
Let's look at the application of the bitwise operator. Let's say we have an array in which every number is repeated twice except for one number that occurs only once. We need to find that unique number. There can be different approaches to this problem but an efficient method would be to XOR all elements of the array. Let's see this with an example,

Say we have an array with the elements: 1,5,6,2,5,6,3,2,3

Clearly, the unique number is 1.

If we XOR all these numbers together due to the same bits in the repeated numbers, they will give 0.

5^5=6^6=3^3=2^2=0.

And, when we XOR 1 and 0, we'll get 1. This way we can easily find the unique number.

Let's implement this solution,

function findUnique(arr){
	var ans=0;
	for(let i=0; i<arr.length; i++)
		ans=ans^arr[i];
	return ans;
}

JavaScript Tutorial »